YAIU 非官方营业日志（P4）

「SDOI2019」移动金币

题面：

$1\times n$ $m$ $m$ $m$ 个格子中），则被判定为输家。已经知道 Alice 和 Bob 都是极致聪明的人，他们在任何局面下总能做出最优的操作。那么有多少初始状态能保证 Alice 必胜呢？
$n\le 1.5\times 10^5,m\le 50$ 。

题解：

首先这个等价于一个阶梯 Nim 问题：

阶梯 Nim 问题：有一个楼梯，每个台阶上放了一些金币，每个人每次操作可以选择一级台阶将上面的一些金币放到下一级；不能操作的输。
结论：所有奇数级台阶上的金币数量异或起来就等于这个游戏的 SG 值。
简要证明：偶数级台阶可以是没有用的，因为一个人进行完一次偶数级操作后，另一个人可以再把那些金币放到更下面的一级，抵消这个操作；而操作奇数格相当于删除这些金币。这个思想很有意思。

$\left\lceil\frac{m+1}{2}\right\rceil$ $0$ $n$ $2k\times 2^i$ $\pmatrix{m\\2k}$ 。

AC Submission Click Here!

「ICPC WF 2017」 Money for Nothing

题面：

$n\le 5\times 10^5$ 。

题解：

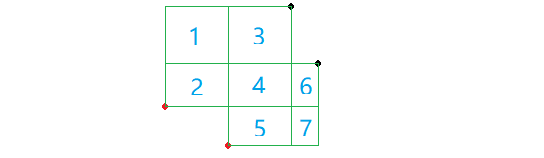
$j$ $x_j\le x_i$ $y_j\le y_i$ $i$ 点就没有用了。我们去掉所有没用的红点和黑点，剩余的图如下：

它并不可二分，比如图中这三个绿色的矩形；但研究一下，它具有决策单调性。即 $i$ $k$ $i-a$ $k+b$ 。如下：

我们有：

S_3+S_4+S_5\ge S_4+S_5+S_6+S_7\\ \Rightarrow S_3\ge S_6+S_7\\ \Rightarrow S_1+S_3\ge S_6\\ \Rightarrow S_1+S_2+S_3+S_4\ge S_2+S_4+S_6\\

$mid$ $x_i<x_j$ $y_i>y_j$ 的，另面积为负数；直接这么做即可了。

AC Submission Click Here!

CF514E Darth Vader and Tree

题面：

$n$ $1 \leq n \leq 10^5$ $i$ $d_i$ $1 \leq d_i \leq 100$ ）。
$x$ $0 \leq x \leq 10^9$ $x$ $10^9+7$ 取模后的结果。

题解：

对于这样一个无限递归的问题，我们直接写出状态转移方程：

dp_j=\sum_{i=1}^ndp_{j-d_i}

直接矩阵快速幂即可。AC Submission Click Here!

CF1428F Fruit Sequences

题面：

$n$ $f$ ，求出：
$\sum_{l=1}^{n}\sum_{r=l}^{n} f(l,r)$
$f(l,r)$ $f[l,r]$ $n\le 5 \times 10^5$ 。

题解：

$O(n)$ $s_i=\sum_{l=1}^i f(l,i)$ $f_i=0$ $s_i=s_{i-1}$ $s_i=s_{i-1}+i-pre$ $pre$ 表示上一处这么多的连续一是在哪个位置。

SPOJ COT3 Combat on a tree

题面：

$n$ 个点的树，每个节点初始时是黑色或白色。
$u$ $1$ $u$ 路径上的所有点染成黑色，谁先无法操作谁输。
$n\le 10^5$ 。

题解：

$SG_u$ $u$ $SG$ 值，于是我写下了第一个假结论：

SG_u=\left(\bigoplus_{s\in son_u}SG_v\right)+1-vl_u

$SG$ $mex$ $SG$ $\boldsymbol{T}_u$ $u$ 子树所有后继状态构成的集合，那么我们可以得到如下的转移方程：

\boldsymbol{T}_u=\bigcup_{s\in son_u}{\left\{x\bigoplus_{t\in son_s,t\neq s}{SG_v} \mid x\in\boldsymbol{T}_v\right\}}

直接用带翻转标记的 01 Trie 合并维护即可；注意一定要带标记，不能在合并时再计算翻转，因为子树下面可能挂着一堆尚未被翻转的点。

solve(u,k) $u$ $k$ 的方案，直接递归下去执行即可。