YAIU 非官方营业日志(1、2、3)
P6383 『MdOI R2』Resurrection
题面:
有一棵包含 个节点的树 ,它的所有边依次编号为 至 。
保证对于 中任意一个节点 ,从 到 号节点的简单路径都不经过任何编号小于 的节点。
按照如下步骤生成一张包含 个节点的无向图 :
选取一个 的排列 ,然后依次进行 次操作。在进行第 次操作时,首先删除树 中编号为 的边 ,然后,记 和 分别为当前树 中与 联通的所有点中,编号最大的点,并在图 的 号点和 号点之间连一条边。
求对于给定的树 ,按上述方式一共可以生成多少种本质不同的图 。图 和 本质不同当且仅当存在 和 满足在 中不存在边 ,而 中存在。
因为答案可能很大,你只需要求出答案对 取模的值。。
题解:
删去边 时(不妨设 ),连的那条边,必然以 为其端点之一;这条边,只能向其祖先连过去。
考虑链的情况,玩一下,发现图应该长如下这样:
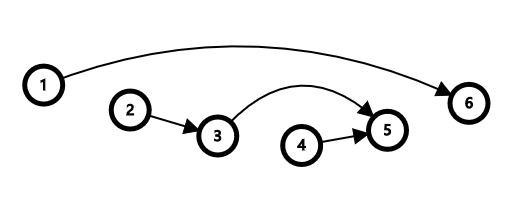
也就是不能相交。证明的话,如果有相交的,显然无解;如果没有相交的,我们直接递归构造。搬到树上也一样的,我们只要数这种连边方式的数量。
那么怎么数呢?树形 dp 有一个惯性是,设 表示 子树内,对上方节点的后效性为 的方案数;在这题中,这个 需要存下向上所有的连边方案,这是行不通的。
我们反过来记录,记下上面对下面的影响。具体来说,我们记 表示,如果上方还有 个点可选(没有被已有的线挡住), 子树内的方案数。那么就很可做了,得到状态转移方程:
CF1592F2 Alice and Recoloring 2
题面:
有一个 的
01矩阵和四种操作:
- 对包含 的一个子矩形作区间翻转,代价为 。
- 对包含 的一个子矩形作区间翻转,代价为 。
- 对包含 的一个子矩形作区间翻转,代价为 。
- 对包含 的一个子矩形作区间翻转,代价为 。
问把一个全 矩阵转换成一个给定矩阵的最小代价。。
题解:
首先我们发现第三、四种操作没有任何作用,都可以换成两个一操作。对原平面做一次二维差分(以 为原点),那么一操作就是一次单点翻转,二操作就是一次四点翻转。
这时一个重要结论是,每一行/列最多被进行一次二操作。否则就会有一半的单点修改没有用,可以直接用一操作来替代,代价不升。一次二操作,只有当 且 且 时,才会对答案起到减一的作用。对于每个满足这个条件的 ,从行 连一条边向 。直接跑二分图最大匹配即可。
点 的影响怎么处理?由于一的代价恰好可以忽略/抵消,我们直接不管它,最后单独判一下即可。,AC Submision Click Here!
P5332 [JSOI2019]精准预测
题面:
目前,火星小镇上有 个居民(编号 )。机器学习算法预测出这些居民在接下来 个时刻(编号)的生死情况,每条预测都是如下两种形式之一:
- 难兄难弟 :在 时刻,如果是死亡状态,那么在 时刻, 是死亡状态。(注意,当 在 时刻是生存状态时,该预测也被认为是正确的);
- 死神来了 :在 时刻,如果 是生存状态,那么在 时刻, 是死亡状态。(注意,当 在 时刻是死亡状态时,该预测也被认为是正确的)。
对于每个人,计算出有多少个人有可能和它一起活到 时刻。,预测条数 。
题解:
对于每个人的每个有效时刻建出两个虚点,显然可以建出一颗 2-SAT。(这里插一句,对于一个限制 别忘了 把 连上,因为这个事调了我好久啊啊啊啊啊)。
那么容易想到的一个结论是, 和 可以共存,当且仅当 且 且 。前两个条件是保证两个分别有解;第三个条件是保证能共存。直接 bitset 传递闭包即可,。
为了空间限制,要分成多个部分分别传递闭包,时间复杂度大体不变;每个点不需要建出其第 时刻。这样就能卡过去了:AC Submision Click Here!
CF932F Escape Through Leaf
题面:
有一颗 个节点的树(节点从 到 依次编号)。每个节点有两个权值,第 个节点的权值为 。
你可以从一个节点跳到它的子树内任意一个节点上。从节点 跳到节点 一次的花费为 。跳跃多次走过一条路径的总费用为每次跳跃的费用之和。请分别计算出每个节点到达树的每个叶子节点的费用中的最小值。
注意:就算树的深度为 ,根节点也不算做叶子节点。另外,不能从一个节点跳到它自己.
,,。
题解:
从一个 的点向 的子树跳,到根的最小代价是一个关于 的一个一次函数构成的下凸壳。我们要做的就是动态维护半平面交合并和单点插入。我们直接李超树合并,复杂度是 的;因为每条直线只会从根一路传递到叶子,均摊一下复杂度就是 的了。AC Submision Click Here!
P5334 [JSOI2019]节日庆典
题面:
对于字符串,定义
其中 是字符串的拼接操作。定义 为最小的 ()满足 (字典序意义下)。
JYY希望你帮助他设计一个算法,让火星人每个节目的气球排列都最美观,即对于给定字符串 的每一个前缀(),求出 。
题解:
感觉是一个比较典型的字符串的推导过程。
我们从左到右依次考虑,设 的答案候选集合为 。将其从小到大排序,由最小性得 是 的一个 Border;如何使限制更加严格呢?设 ,大概会长下面这个样子:
其中, 是 的一个 Border,也是候选集和中的一个元素;容易发现,ABX 一定不会比 AABX 和 BX 都优秀,那么这个 ABX 就没有用了。加上这个剪枝,候选集合的大小就是 级别的了。
维护候选集合直接从左到右暴力地做就好了;那么如何从候选集合中找到答案呢?这就需要快速比较字典序了。由于循环位移比较字典序中需要比的串对中,至少得有一个是前缀,所以可以用 exKMP,求出每个后缀与全串的 lcp,就能 比较字典序啦!AC Submision Click Here!
P5597 [XR-4]复读
题意:
小 X 捡到了一台复读机,这台复读机可以向机器人发号施令。机器人将站在一棵完全二叉树的根上,完全二叉树是无限延伸的。你将向复读机录入一串指令,这串指令单个字符可以是:
L:命令机器人向当前节点的左子走;R:命令机器人向当前节点的右子走;U:命令机器人向当前节点的父亲走(若没有,则命令非法)。录入指令后,复读机将会把指令无限复读下去。比如命令为
LR,那么机器人会遵从LRLRLRLR...一直走下去。这棵完全二叉树上有一个 个节点的连通块,保证这个连通块包含根节点。连通块上的每个节点都埋有宝藏,机器人到达过的地方如果有宝藏,则会将其开采。如果一个地方没有宝藏,机器人也可以到那里去。机器人也可以反复经过一个地方。
显然,这个连通块本身也是一棵二叉树。
现在,有人告诉了小 X 埋有宝藏的这棵二叉树的前序遍历,小 X 需要寻找到一条尽量短的指令,使得机器人能够挖掘出所有宝藏。
题解:
枚举一个周期的位移矢量,然后会把原树分成很多段,求个并即可。没什么好解释的,就是码就好了。AC Submision Click Here!
P3293 [SCOI2016]美味
题面:
一家餐厅有 道菜,编号 ,大家对第 道菜的评价值为 。有 位顾客,第 位顾客的期望值为 ,而他的偏好值为 。因此,第 位顾客认为第 道菜的美味度为 , 表示异或运算。
第 位顾客希望从这些菜中挑出他认为最美味的菜,即美味值最大的菜,但由于价格等因素,他只能从第 道到第 道中选择。请你帮助他们找出最美味的菜。
题解:
我们建出可持久化值域线段树,用于查询一个区间内是否存在值域在某个范围内的数。然后我们从高到低位考虑,每次查的都是一个区间,逐渐缩小范围,直到确定这个数。。AC Submision Click Here!
P4898 [IOI2018] seats 排座位
题面:
你要在一个长方形大厅里举办国际编程比赛,该大厅共有 个座位( 行 列)。行的编号是从 到 ,列的编号是从 到 。位于 行 列的座位用 表示。一共邀请了 位参赛者,编号是从 到 。你制定好了一个座位表,第 个参赛者被安排到座位 。座位表中参赛者和座位是一一对应的。
大厅中一个座位集合 被称为是长方形的,如果存在整数 和 满足下列条件:
- 。
- 。
- 正好是所有满足 和 的座位 的集合。
如果一个长方形座位集合包含 个座位,并且被分配到这个集合的参赛者的编号恰好是从 到 ,那么该集合是美妙的。一个座位表的美妙度定义为这个表中美妙的长方形座位集合的个数。
在准备好座位表后,你会收到一些交换两个参赛者座位的请求。具体来说,有 个这样的请求,按时间顺序编号为 到 。第 个请求希望交换参赛者 和 的座位。你立即接受每个请求并更新座位表。每次更新后,你的目标是计算当前座位表的美妙度。
题解:
在 Chen_03 的循循善诱下做出了这道题。
先考虑只有一列的情况。我们肯定是要对人的编号为下标的序列维护一个什么东西,这个东西能够判定是否连通且能方便地求和。设 为第 个人的位置,那么我们判断 能构成美妙集合当且仅当:
我们建一个以人的编号为下标的线段树,维护每个 ;考虑插入一个数作为 的贡献,那么它对应着一个区间加。统计最小值个数即可。
二维情况怎么办?如下:
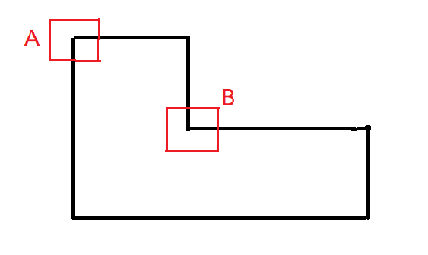
我们直接统计 的数量和 的数量; 必须一个都没有,权值设为 ; 必须有恰好 个,权值设为 ,直接维护一个编号上的线段树即可。